Neutrino mass ordering

In this page we briefly resume the status of the mass ordering presented here and updated here.
The results of the global analysis are here.

Masses and ordering

The neutrino masses can be ordered in two ways:

normal ordering (NO): the lightest neutrino is 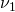$\nu_1$ , the one with the largest mixing with the electron neutrino flavor, and $\Delta m^2_{31}>0$ ;
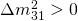inverted ordering (IO): the lightest neutrino is 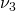$\nu_3$ , the one with the smallest mixing with the electron neutrino flavor, and $\Delta m^2_{31}<0$ .

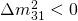The mass ordering can be determined measuring the sign of $\Delta m^2_{31}$ or singling out each of the masses of the three neutrino mass eigenstates.
Indirect constraints may also come from the observation of the neutrinoless double beta decay or from cosmological bounds on the sum of the neutrino masses (which must be larger than 0.06 eV in NO or than 0.1 eV in IO).

Neutrino oscillations

Neutrino oscillation experiments can only determine the mass ordering through neutrino oscillations in matter, in particular exploiting matter effects inside Earth.
Current classes of experiments that can do so include atmospheric or long baseline accelerator experiments.
At the moment, the experiments that have some sensitivity on the mass ordering are SuperKamiokande, NO $\nu$ A, T2K.
Global fits combining these and the other neutrino oscillation experiments give nowadays a preference of $\Delta\chi^2\simeq 6.4$ between IO and NO, thus corresponding to a $2.5\sigma$ preference in favor of normal ordering.

Neutrinoless double beta decay

Only allowed for Majorana neutrinos, neutrinoless double beta decay ( $0\nu\beta\beta$ ) is a process that permits to determine a combination of the neutrino masses, the effective Majorana mass:

$m_{\beta\beta}=\sum_{k=1}^N e^{i\alpha_k}|U_{ek}|^2 m_k$

.
As the value of $m_{\beta\beta}$ may depend on the mass ordering (if the lightest neutrino is lighter than $\sim40\mbox{ meV}$ ), a determination of the mass ordering may come from a detection of the neutrinoless double beta decay process.

In the analysis, we adopt constraints from KamLAND-ZEN (paper), GERDA (paper) and CUORE (paper) on the half-life of the neutrinoless double beta decay process.

Current generation experiments do not have a sufficient precision to be competitive in constraining the neutrino mass ordering.

Cosmology

Cosmological probes can nowadays constrain the neutrino masses only through their sum, $\sum m_\nu$ . Since the known mass splittings $\Delta m^2_{21}$ and $\Delta m^2_{31}$ force $\sum m_\nu^{\rm NO}\gtrsim0.06\mbox{ eV}$ and $\sum m_\nu^{\rm IO}\gtrsim0.1\mbox{ eV}$ , a strong bound on $\sum m_\nu$ could in principle be used to severely constrain or eventually rule out the IO case.

At the current level, the cosmological bounds are not strong enough to give a statistically significant preference for one of the orderings, as the strongest limits correspond to odds of $\sim 3.3:1$ in favor of NO.
In our analyses we use Cosmic Microwave Background (CMB) data from Planck and Baryon Acoustic Oscillation (BAO) data from various experiments in order to derive constraints on $\sum m_\nu$ and the corresponding preference in favor of NO. The cosmological dataset including CMB and BAO data, indicated with “Cosmo”, should be considered as conservative.
When we additionally include a prior from local determinations of the $H_0$ parameter ( $H_0=74.04\pm1.42\mbox{ km s}^{-1}\mbox{ Mpc}^{-1}$ ), the analysis becomes less conservative and slightly stronger bounds can be derived.

(Bayesian) global fit

We perform a global Bayesian analysis combining the various datasets described above. The neutrino mass sector is parameterized using linear priors in $\log_{10}m_{\rm lightest}$ , $\Delta m^2_{21}$ and $\Delta m^2_{31}$ , since our previous paper demonstrated that these three parameters represent the most efficient way to sample the parameter space.

We compute the Bayesian evidence of the NO and IO cases using different data combinations and we use them to compute the Bayes factors of NO versus IO, which allow us to quantify the preference for one of the two orderings.

Driven by the results coming from neutrino oscillation data, the preference is always in favor of NO.
Using the Jeffreys’ scale, this preference can be quantified as moderate, in particular corresponding to something more than $2.0\sigma$ , as reported in this table, from this paper:

Data combination	Bayes factor NO vs IO	$N\sigma$
OSC	$3.01\pm0.04$	$2.0\sigma$
OSC+ $\beta$	$3.22\pm0.03$	$2.1\sigma$
OSC+ $0\nu\beta\beta$	$3.46\pm0.25$	$2.2\sigma$
OSC+Cosmo	$4.90\pm0.50$	$2.7\sigma$
OSC+Cosmo+ $H_0$	$4.98\pm0.34$	$2.7\sigma$